3次の自然スプライン補間を Python でスクラッチ実装したサンプルを掲載します。
通常は scipy あたりの CubicSpline を利用することで事足りるかと思います。
やむなき事情で、スプライン補間のプリミティブな実装例がほしいときのための参考です。
アルゴリズムは以下の Wikipedia の記載を参考にしています。
次のような補間方法のサンプルです。
- 3次のスプライン補間
- 端点における二次微分をゼロとする、自然スプライン補間
- 補外部分は直線で延長
スプライン補間のスクラッチ実装サンプル
import matplotlib.pyplot as plt
def natural_cubic_spline(xs, ys):
n = len(xs)
a = [y for y in ys] # deepcopy
h = [xs[i + 1] - xs[i] for i in range(n - 1)]
alpha = [
3 / h[i + 1] * (a[i + 2] - a[i + 1]) - 3 / h[i] * (a[i + 1] - a[i])
for i in range(n - 2)
]
l = [1] * n
mu = [0] * (n - 1)
z = [0] * n
for i in range(1, n - 1):
l[i] = 2 * (xs[i + 1] - xs[i - 1]) - h[i - 1] * mu[i - 1]
mu[i] = h[i] / l[i]
z[i] = (alpha[i - 1] - h[i - 1] * z[i - 1]) / l[i]
b = [0] * n
c = [0] * n
d = [0] * (n - 1)
for i in range(n - 2, -1, -1):
c[i] = z[i] - mu[i] * c[i + 1]
b[i] = (a[i + 1] - a[i]) / h[i] - h[i] * (c[i + 1] + 2 * c[i]) / 3
d[i] = (c[i + 1] - c[i]) / (3 * h[i])
b[n - 1] = b[n - 2] + 2 * c[n - 2] * h[-1] + 3 * d[n - 2] * h[-1] ** 2
xs = [x for x in xs] # deepcopy
def f(x):
if x <= xs[0]:
return a[0] + b[0] * (x - xs[0])
if xs[-1] <= x:
return a[-1] + b[-1] * (x - xs[-1])
for i in range(n - 1):
if xs[i + 1] < x:
continue
h = x - xs[i]
return a[i] + b[i] * h + c[i] * h**2 + d[i] * h**3
return f
xs = [0, 1, 2, 10]
ys = [1, 3, 2, 4]
f = natural_cubic_spline(xs, ys)
extra = 2
xmin = xs[0] - extra
xmax = xs[-1] + extra
n = 100
x_sampled = [xmin + (xmax - xmin) * i / n for i in range(n + 1)]
y_sampled = [f(x) for x in x_sampled]
plt.plot(x_sampled, y_sampled)
plt.plot(xs, ys, ".r", markersize=10)
plt.show()
補間のプロット例
出力をプロットすると次のようになります。
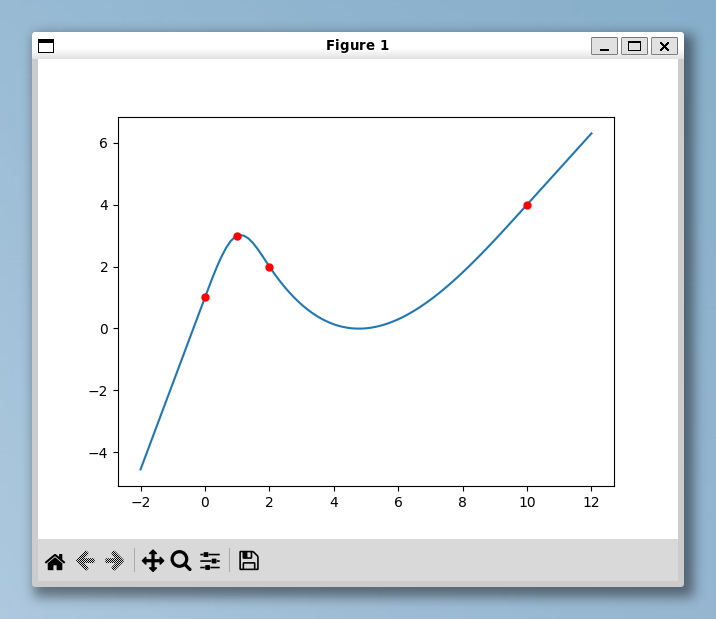
scipy を利用する場合
scipy を利用する例も掲載しておきます。
通常利用はこれで十分と思います。
from scipy.interpolate import CubicSpline
import matplotlib.pyplot as plt
xs = [0, 1, 2, 10]
ys = [1, 3, 2, 4]
f = CubicSpline(xs, ys, bc_type="natural")
extra = 2
xmin = xs[0] - extra
xmax = xs[-1] + extra
n = 100
x_sampled = [xmin + (xmax - xmin) * i / n for i in range(n + 1)]
y_sampled = f(x_sampled)
plt.plot(x_sampled, y_sampled)
plt.plot(xs, ys, ".r", markersize=10)
plt.show()
補外方法は、端点の三次曲線をそのまま延長したものになっています。
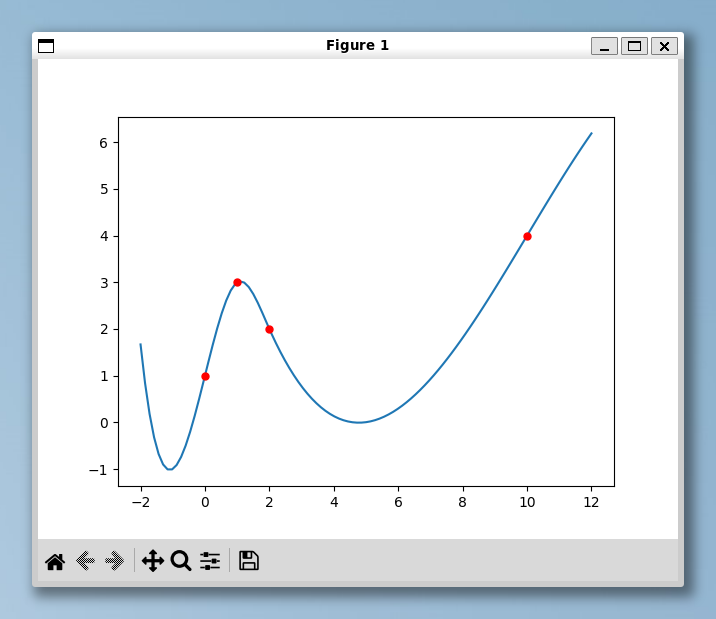







コメント