二次元平面において、任意の点列を補間するアルゴリズムが多種あります。
その中でも、自然スプライン補間では、各点を滑らかに結合することのできるアルゴリズムです。
三次スプラインで生成した曲線には次のような特徴があります。
- インプットとなる点を必ず通る
- 滑らかな関数である（関数が連続であり、かつ任意の点で微分可能である）
この記事では、C++ での自然スプライン補間の実装例を掲載します。
目次
自然スプライン補間の実装例
事前準備 – 補間計数の算出
自然スプライン補間では、任意の点列を次のような三次関数で補間します。
$$
S_i(x) = a_i + b_i(x – x_i) + c_i(x – x_i)^2 + d_i(x – x_i)^3
$$
まず最初に、上記式の計数 \(a_i, b_i, c_i, d_i, x_i\) を求める必要があります。
\(x_i\) は、インプットとなる点列の \(x_i\) そのものです。
\(a_i\) も同様に、インプットとなる点列の \(y_i\) と同じ値となります。
それ以外の \(b_i, c_i, d_i\) については、以下の wikipedia を参考に計算を実装しています。
#include <algorithm>
#include <iostream>
#include <vector>
class NaturalCubicSplineInterpolator
{
public:
NaturalCubicSplineInterpolator(
std::vector<double> &&a,
std::vector<double> &&b,
std::vector<double> &&c,
std::vector<double> &&d,
std::vector<double> &&x)
: a_(std::move(a)), b_(std::move(b)), c_(std::move(c)), d_(std::move(d)), x_(std::move(x))
{
}
double operator()(double x) const
{
// 補間処理はあとで掲載
}
static NaturalCubicSplineInterpolator from_points(
const std::vector<std::pair<double, double>> &ps)
{
std::size_t n = ps.size();
std::vector<double> x;
std::transform(
ps.begin(), ps.end(), std::back_inserter(x), [](const auto &p)
{ return p.first; });
std::vector<double> y;
std::transform(
ps.begin(), ps.end(), std::back_inserter(y), [](const auto &p)
{ return p.second; });
std::vector<double> a(y);
std::vector<double> h;
for (std::size_t i = 0; i < n - 1; ++i)
{
h.push_back(x[i + 1] - x[i]);
}
std::vector<double> alpha(n - 1);
for (std::size_t i = 1; i < n - 1; ++i)
{
alpha[i] = 3.0 * (a[i + 1] - a[i]) / h[i] - 3.0 * (a[i] - a[i - 1]) / h[i - 1];
}
std::vector<double> l(n);
std::vector<double> mu(n - 1);
std::vector<double> z(n);
l[0] = 1.0;
mu[0] = 0.0;
z[0] = 0.0;
for (std::size_t i = 1; i < n - 1; ++i)
{
l[i] = 2.0 * (x[i + 1] - x[i - 1]) - h[i - 1] * mu[i - 1];
mu[i] = h[i] / l[i];
z[i] = (alpha[i] - h[i - 1] * z[i - 1]) / l[i];
}
l[n - 1] = 1.0;
z[n - 1] = 0.0;
std::vector<double> b(n);
std::vector<double> c(n);
std::vector<double> d(n - 1);
c[n - 1] = 0.0;
for (std::size_t i = n - 1; i--;)
{
c[i] = z[i] - mu[i] * c[i + 1];
b[i] = (a[i + 1] - a[i]) / h[i] - h[i] * (c[i + 1] + 2.0 * c[i]) / 3.0;
d[i] = (c[i + 1] - c[i]) / (3.0 * h[i]);
}
b[n - 1] = b[n - 2] + h[n - 2] * (2.0 * c[n - 2] + 3.0 * d[n - 2] * h[n - 2]);
return NaturalCubicSplineInterpolator(
std::move(a), std::move(b), std::move(c), std::move(d), std::move(x));
}
private:
std::vector<double> a_;
std::vector<double> b_;
std::vector<double> c_;
std::vector<double> d_;
std::vector<double> x_;
};補間計算
ここまでできたら、あとは \(S_i(x)\) の式を実装するだけです。
補間クラスのインスタンスに対して、() 演算子を呼び出すことで補間計算ができるようになります。
class NaturalCubicSplineInterpolator
{
public:
// 省略
double operator()(double x) const
{
if (x <= x_.front())
{
return a_.front() + b_.front() * (x - x_.front());
}
if (x_.back() <= x)
{
return a_.back() + b_.back() * (x - x_.back());
}
for (std::size_t i = 0; i < x_.size() - 1; ++i)
{
if (x_[i + 1] <= x)
{
continue;
}
double h = x - x_[i];
return a_[i] + h * (b_[i] + h * (c_[i] + h * d_[i]));
}
throw std::runtime_error("unexpected error");
}
// 省略
};補間実行例
上記のクラスを利用して、実際に補間を計算させるサンプルです。
\((0, 0), (2, 2), (3, 1), (6, 3), (10, -1)\) の5点をインプットとしています。
int main()
{
const std::vector<std::pair<double, double>> ps{
{0.0, 0.0},
{2.0, 2.0},
{3.0, 1.0},
{6.0, 3.0},
{10.0, -1.0},
};
const auto interpolator = NaturalCubicSplineInterpolator::from_points(ps);
// 入力点 X の表示
for (const auto &p : ps)
{
std::cout << p.first << " ";
}
std::cout << std::endl;
// 入力点 Y の表示
for (const auto &p : ps)
{
std::cout << p.second << " ";
}
std::cout << std::endl;
std::size_t n = 200;
double x_min = -1.0;
double x_max = 11.0;
double h = (x_max - x_min) / (n - 1);
// 出力点 X の表示
for (std::size_t i = 0; i < n; ++i)
{
std::cout << (x_min + i * h) << " ";
}
std::cout << std::endl;
// 出力点 Y の表示
for (std::size_t i = 0; i < n; ++i)
{
std::cout << interpolator(x_min + i * h) << " ";
}
std::cout << std::endl;
return 0;
}この main 関数を実行すると、次の数列が合計4行出力されます。
- 入力\(x_i\)
- 入力\(y_i\)
- 出力\(x_i\)
- 出力\(y_i\)
$ g++ natural_cubic_spline.cc && ./a.out
0 2 3 6 10
0 2 1 3 -1
-1 -0.939698 -0.879397 -0.819095 -0.758794 -0.698492 -0.638191 -0.577889 -0.517588 -0.457286 -0.396985 -0.336683 -0.276382 -0.21608 -0.155779 -0.0954774 -0.0351759 0.0251256 0.0854271 0.145729 0.20603 0.266332 0.326633 0.386935 0.447236 0.507538 0.567839 0.628141 0.688442 0.748744 0.809045 0.869347 0.929648 0.98995 1.05025 1.11055 1.17085 1.23116 1.29146 1.35176 1.41206 1.47236 1.53266 1.59296 1.65327 1.71357 1.77387 1.83417 1.89447 1.95477 2.01508 2.07538 2.13568 2.19598 2.25628 2.31658 2.37688 2.43719 2.49749 2.55779 2.61809 2.67839 2.73869 2.79899 2.8593 2.9196 2.9799 3.0402 3.1005 3.1608 3.22111 3.28141 3.34171 3.40201 3.46231 3.52261 3.58291 3.64322 3.70352 3.76382 3.82412 3.88442 3.94472 4.00503 4.06533 4.12563 4.18593 4.24623 4.30653 4.36683 4.42714 4.48744 4.54774 4.60804 4.66834 4.72864 4.78894 4.84925 4.90955 4.96985 5.03015 5.09045 5.15075 5.21106 5.27136 5.33166 5.39196 5.45226 5.51256 5.57286 5.63317 5.69347 5.75377 5.81407 5.87437 5.93467 5.99497 6.05528 6.11558 6.17588 6.23618 6.29648 6.35678 6.41709 6.47739 6.53769 6.59799 6.65829 6.71859 6.77889 6.8392 6.8995 6.9598 7.0201 7.0804 7.1407 7.20101 7.26131 7.32161 7.38191 7.44221 7.50251 7.56281 7.62312 7.68342 7.74372 7.80402 7.86432 7.92462 7.98492 8.04523 8.10553 8.16583 8.22613 8.28643 8.34673 8.40704 8.46734 8.52764 8.58794 8.64824 8.70854 8.76884 8.82915 8.88945 8.94975 9.01005 9.07035 9.13065 9.19095 9.25126 9.31156 9.37186 9.43216 9.49246 9.55276 9.61307 9.67337 9.73367 9.79397 9.85427 9.91457 9.97487 10.0352 10.0955 10.1558 10.2161 10.2764 10.3367 10.397 10.4573 10.5176 10.5779 10.6382 10.6985 10.7588 10.8191 10.8794 10.9397 11
-1.77594 -1.66885 -1.56175 -1.45466 -1.34757 -1.24048 -1.13339 -1.0263 -0.919204 -0.812112 -0.705021 -0.597929 -0.490837 -0.383745 -0.276654 -0.169562 -0.0624702 0.0446185 0.151592 0.258205 0.3642 0.469324 0.57332 0.675934 0.776911 0.875994 0.97293 1.06746 1.15934 1.2483 1.33409 1.41645 1.49514 1.5699 1.64046 1.70658 1.768 1.82446 1.87571 1.9215 1.96156 1.99565 2.02351 2.04488 2.05951 2.06714 2.06752 2.0604 2.0455 2.0226 1.99142 1.95209 1.90548 1.85253 1.79417 1.73134 1.665 1.59608 1.52552 1.45426 1.38326 1.31344 1.24574 1.18113 1.12052 1.06487 1.01511 0.972137 0.936157 0.90695 0.884291 0.867952 0.857707 0.85333 0.854592 0.861268 0.873131 0.889954 0.91151 0.937573 0.967915 1.00231 1.04053 1.08235 1.12754 1.17588 1.22714 1.28109 1.33751 1.39616 1.45683 1.51928 1.58329 1.64863 1.71507 1.7824 1.85037 1.91877 1.98737 2.05594 2.12425 2.19208 2.2592 2.32538 2.3904 2.45404 2.51605 2.57622 2.63432 2.69013 2.74341 2.79394 2.84149 2.88584 2.92676 2.96402 2.9974 3.0267 3.05193 3.07315 3.09043 3.10381 3.11337 3.11917 3.12127 3.11974 3.11463 3.106 3.09393 3.07847 3.05968 3.03763 3.01237 2.98398 2.95251 2.91803 2.8806 2.84027 2.79712 2.7512 2.70258 2.65132 2.59748 2.54112 2.48231 2.42111 2.35758 2.29178 2.22377 2.15363 2.0814 2.00715 1.93095 1.85285 1.77293 1.69123 1.60783 1.52278 1.43615 1.348 1.25839 1.16738 1.07504 0.981435 0.886617 0.790653 0.693603 0.595532 0.496501 0.396573 0.295809 0.194272 0.0920241 -0.0108722 -0.114355 -0.218361 -0.32283 -0.427698 -0.532903 -0.638383 -0.744076 -0.849919 -0.955851 -1.06181 -1.16777 -1.27373 -1.37969 -1.48565 -1.59161 -1.69757 -1.80353 -1.90949 -2.01545 -2.12141 -2.22737 -2.33333 -2.43929 -2.54525 -2.65121 -2.75717 グラフ出力
標準出力してもわかりづらいので、Python の matplotlib で補間結果のグラフを出力させます。
import matplotlib.pyplot as plt
x_in = [float(x) for x in input().split()]
y_in = [float(y) for y in input().split()]
x_out = [float(x) for x in input().split()]
y_out = [float(y) for y in input().split()]
fig, ax = plt.subplots()
ax.plot(x_in, y_in, ".", color="tab:blue", markersize=10)
ax.plot(x_out, y_out, color="tab:blue")
plt.show()
C++ の標準出力をそのまま python にパイプすることでグラフの描画が可能です。
$ g++ natural_cubic_spline.cc && ./a.out | python3 plot.py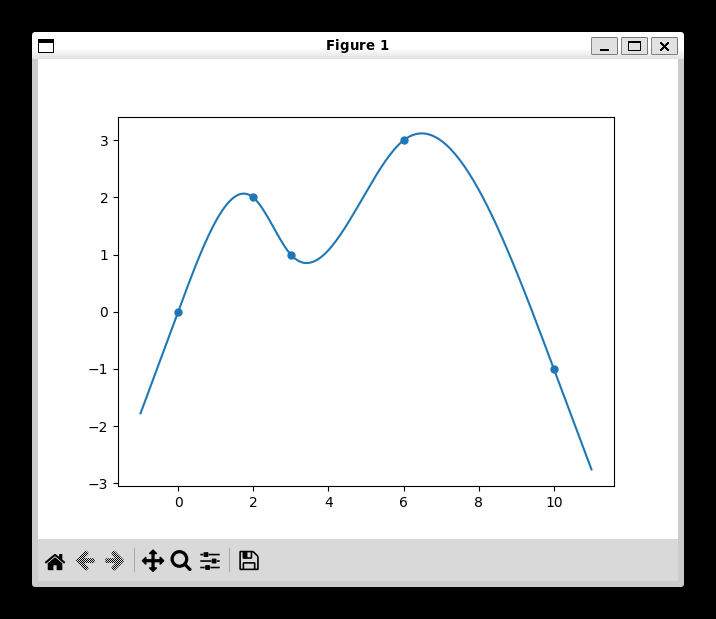 
関連記事 – WSL で matplotlib を利用する
WSL で matplotlib を利用するための関連記事も掲載しておきます。
あわせて読みたい
WSL – Python matplotlib でグラフを描画する
Python では matplotlib パッケージを利用して多様なグラフを描画することができます。この記事では、WSL の Ubuntu にて matplotlib を実行する方法をまとめます。 Lan…
コメント